软件介绍
matlabAPP简介
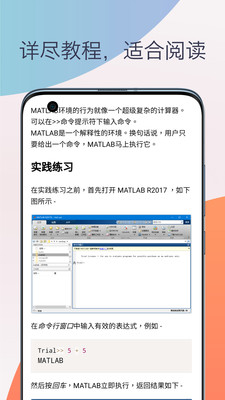
MATLAB教程app的最新版本是专门为MATLAB初学者设计的,它为用户提供了许多独特的学习方法、多样化的教程资源和自定义的配置功能。这些特点使得MATLAB教程app成为学习MATLAB的理想工具。这个app提供了一种独特的学习方法,将MATLAB语言的理论知识和实践操作相结合。感兴趣的小伙伴快来本站下载吧。
matlabAPP亮点
面向初学者:软件针对MATLAB初学者设计,提供易于学习的教程和操作指南;
独特的学习方法:软件提供独特的学习方法,结合了理论知识和操作实践;
配置灵活:软件支持自定义配置,让用户可以灵活调整软件界面和功能,以满足不同需求。

matlabAPP特色
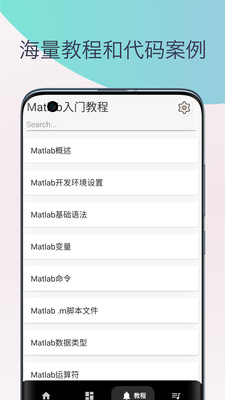
教程学习:软件提供各种学习教程,包括MATLAB基本操作、数学建模等,方便用户进行深入学习;
实例操作:软件提供多种MATLAB语言实例和实践操作,让用户可以通过实际操作来提高自己的MATLAB应用能力;
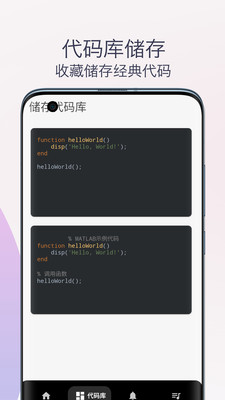
交流社区:软件提供在线交流社区,用户可以在此分享和交流MATLAB学习经验和技巧。

Matlab化简表达式/多项式的操作教程

相关指令简介
这儿介绍下采用公因子发简化表达式的相关置换指令。气质要的函数指令为:“subexpr”。subexpr是替换表达式命令。在很多特繁琐的解析表达式中,常有个在不同地方重复出现的表达式,此时用simple或simplify都无法化简,而用这个命令就能得到效果很好的简化结果。下面说下subexpr指令的语法规则:
RS=subexpr(expr) expr为表达式,其表示从expr中提取出公因子sigma,并且将采用sigma重写的expr表达式赋给RS;
RS=subexpr(expr,'s') 从expr中提取出公因子,记为S,并将用S重写的expr赋给RS;这里能指定公因子的名称为'S'
[RS,s]=subexpr(expr,'s') 该调用语法的效果和上一句“RS=subexpr(expr,'s')”是一样的。
注意,expr可以是符号表达式或符号表达式矩阵。此外还可以应用help指令学习subexpr的用发,结果如下图:
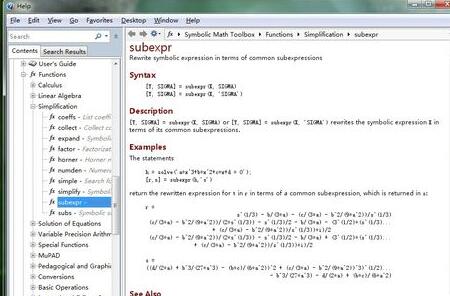
公因子法简化表达式
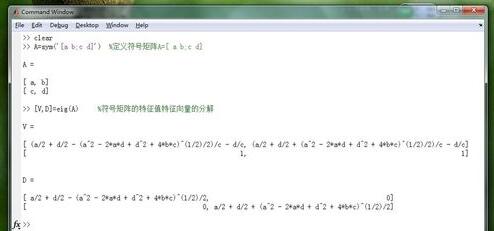
至于用公因子法简化表达式,采用对符号矩阵A=[ a b;c d]进行特征向量分解的实例来演示,以演示cubexpr的正确用法,实例演示复杂符号矩阵的公因子法化简。这里我们需要生成符号矩阵。如图所示:

特征值和特征向量
当生成符号矩阵后,就需对上一步的符号矩阵进行特征之和特征向量分解。这里我们要用到“eig”函数,其用法是:[V,D]=eig(A),求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成矩阵V。下面就用这条指令求第二步符号矩阵的特征值和特征向量,如图所示:
自动识别表达式中的公因子
下面开始使用subexpr函数指令进行公因子识别了,注意subexpr函数的具体应用哦!这里先使用一下第一步用法中的第一条,具体如图所示:
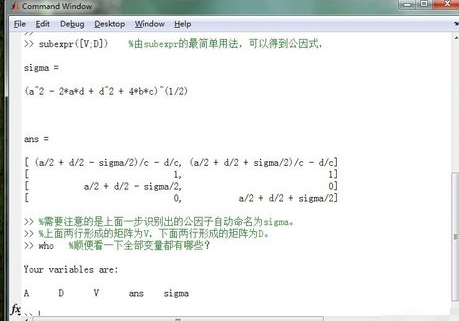
对D进行“指定公因子名称”的简化
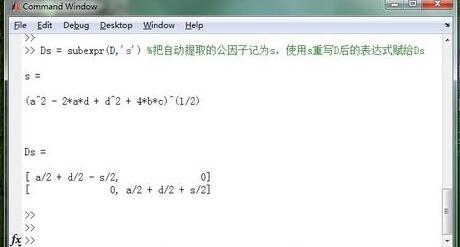
下面探索一下subexpr函数指令的另一个用法,即对提取的公因子制定名称,即把从D中提取出的公因子命名为s,然后用s重写的D赋给Ds;这里能指定公因子的名称为's'。代码:Ds=subexpr(D,'s') ;具体如图所示:
对V、D同时简化,并且制定相同的公因式名称
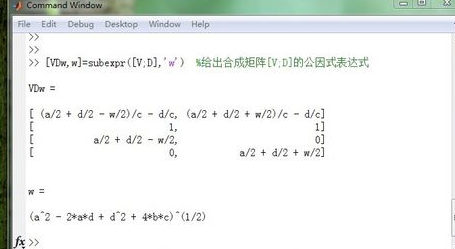
下面将V、D合成为一个矩阵,然后同时对矩阵[V;D]提取公因式,这时将公因式命名为w,并用w重写矩阵[V;D]并命名为VDw。代码指令:[VDw,w]=subexpr([V;D],'w') ,具体结果如图所示:
学完本文Matlab化简表达式/多项式的操作内容,是不是觉得以后操作起来会更容易一点呢?
matlabAPP测评
MATLAB教程app最新版是一款专为MATLAB初学者设计的学习工具。它独特的学习方法、多样化的教程资源和自定义的配置功能,使得学习MATLAB变得更加简单、高效和有趣。无论您是刚刚开始学习MATLAB,还是已经有一定基础的用户,都可以从这个app中获益良多。